BER of 3 user Non-orthogonal multiple access (NOMA) with QPSK modulation

Next post: Single Carrier NOMA - How many users can it support?

In a previous post, we saw how to plot the bit error rate (BER) of a two user NOMA. There, we used BPSK modulation for both the users. Can we multiplex more than two users in a single carrier in NOMA? Of course. In this post, we are going to multiplex three users, each following QPSK modulation, in a single frequency carrier.

Download MATLAB code for 3 user NOMA here

System Model

Let us consider a wireless network consisting of three NOMA users, numbered U1, U2 and U3. Let $d_1$, $d_2$ and $d_3$ denote their respective distances from the base station (BS) such that, $d_1 \gt d_2 \gt d_3$. Based on their distances, U1 is the weakest/farthest user and U3 is the strongest/nearest user to the BS. 

Let $h_1$, $h_2$, and $h_3$ denote their corresponding Rayleigh fading coefficients such that, $|h_1|^2 \lt |h_2|^2 \lt |h_3|^2$ . (The channels are ordered this way because $h_i \propto \dfrac{1}{d_i}$)

Let $\alpha_1$, $\alpha_2$ and $\alpha_3$ denote their respective power allocation coefficients. According to the principles of NOMA, the weakest user must be allocated the most power and the strongest user must be allocated the least power. Therefore, the power allocation coefficients must be ordered as $\alpha_1 \gt \alpha_2 \gt \alpha_3$. The choice of power allocation coefficients has a great significance on the performance of a NOMA network. In this post, for simplicity, we are using fixed power allocation. There are several dynamic power allocation schemes available, that would give better performance.

Signal Model

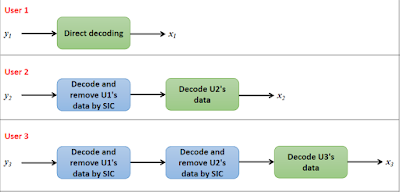
Let $x_1$, $x_2$ and $x_3$ denote the QPSK modulated messages that the BS needs to send to U1, U2 and U3 respectively. Then, the superposition coded signal transmitted by the BS is given by, $$x = \sqrt{P}(\sqrt{\alpha_1}x_1+\sqrt{\alpha_2}x_2+\sqrt{\alpha_3}x_3)$$ The signal received at the $i^{th}$ user is given by, $$y_i = h_ix + n_i$$ where $n_i$ denotes AWGN at receiver of Ui.

SIC Decoding procedure

At User 1

Since U1 is allocated the highest power, he will perform direct decoding from $y_1$, treating the signals of U2 and U3 as interference. Thus, the achievable rate of U1 is, $$R_1 = log_2\left(1 + \dfrac{\alpha_1P|h_1|^2}{\alpha_2P|h_1|^2+\alpha_3P|h_1|^2+\sigma^2}\right)$$ which can further be simplified as, $$R_1 = log_2\left(1 + \dfrac{\alpha_1P|h_1|^2}{(\alpha_2+\alpha_3)P|h_1|^2+\sigma^2}\right)$$ From the above equation, we make one important observation. Since $\alpha_2 + \alpha_3$ is present at the denominator, now we want $\alpha_1$ to satisfy $\alpha_1 \gt \alpha_2 + \alpha_3$. Only then, U1's power will dominate in the transmit signal, $x$ and in the received signal, $y_1$.

At User 2

Next let's write the rate equation for U2. Since $\alpha_2 \lt \alpha_1$ and, $\alpha_2 \gt \alpha_3$, U2 must perform successive interference cancellation to remove U1's data and treat U3 as interference. After removing U1's data by SIC, the achievable rate for U2 is, $$R_2 = log_2\left(1 + \dfrac{\alpha_2P|h_2|^2}{\alpha_3P|h_2|^2 + \sigma^2}\right)$$ Since $\alpha_3$ is present in the interference term at the denominator, we want $\alpha_2$ to satisfy $\alpha_2 \gt \alpha_3$.

At User 3

Finally, U3 ($\alpha_3 \lt \alpha_1$, $\alpha_3 \lt \alpha_2$,) has to perform SIC two times to remove both U1 and U2 data from $y_3$. Since the $\alpha_1$ term dominates in $y_3$, it must be removed first. After that, the $\alpha_2$ term must be removed. The achievable rate is, $$R_3 = log_2\left(1 + \dfrac{\alpha_3P|h_3|^2}{\sigma^2}\right)$$ 

MATLAB Simulation

Let's simulate the BER vs transmit power characteristics of this system using MATLAB. 

Download MATLAB code for 3 user NOMA here

1. First, let's set our simulation parameters: Distances are set as $d_1 = 500m$, $d_2 = 200m$, $d_3 = 70m$. The power allocation coefficients are set as $\alpha_1=0.8$, $\alpha_2 = 0.15$, $\alpha_3 = 0.05$. These values satisfy the conditions $\alpha_1 \gt \alpha_2 \gt \alpha_3$ and, $\alpha_1 \gt \alpha_2 + \alpha_3$.  Set path loss exponent.

        d1 = 500; d2 = 200; d3 = 70;       %Set distances
        a1 = 0.8; a2 = 0.15; a3 = 0.05;    %Power allocation coefficients 

        eta = 4;                           %Path loss exponent

2. Set the transmit power range (here, we have used 0 to 40 dBm). Convert the transmit power from dBm to linear scale for future calculations.

        Pt = 0:40                   %Transmit power in dBm
        pt = (10^-3)*db2pow(Pt);    %Transmit power in linear scale    

3. Generate Rayleigh fading coefficients $h_1$, $h_2$, $h_3$ for each user using the command: 

        h1 = sqrt(d1^-eta)*(randn(N/2,1) + 1i*randn(N/2,1))/sqrt(2);
        h2 = sqrt(d2^-eta)*(randn(N/2,1) + 1i*randn(N/2,1))/sqrt(2);
        h3 = sqrt(d3^-eta)*(randn(N/2,1) + 1i*randn(N/2,1))/sqrt(2);

Here, N is the number of bits to be transmitted. Since we are using QPSK modulation, each symbol has 2 bits. Therefore, we are going to transmit N/2 symbols. For each symbol, we are generating a Rayleigh fading coefficient. 

Also, $d_i^{-\eta}$ is the variance of $h_i$, and its mean is zero

4. Define the amount of noise power. For that, let's consider a bandwidth of 1 MHz. As we know, the thermal noise power is given by, kTB. For a bandwidth of 1 Hz, the noise power is $log_{10}(kT) = - 174$ dBm. So, for 1 MHz bandwidth, the noise power will be $-174 + log_{10}(1MHz)$.

        BW = 10^6;                    %Bandwidth
        No = - 174 + 10*log10(BW);    %Noise power in dBm
        no = (10^-3)*db2pow(No);      %Noise power in linear scale

5. Using the noise power calculated in step 3, let's generate noise samples for all the three users by using the following command:

        n1 = sqrt(no)*(randn(N/2,1) + 1i*randn(N/2,1))/sqrt(2);
        n2 = sqrt(no)*(randn(N/2,1) + 1i*randn(N/2,1))/sqrt(2);
        n3 = sqrt(no)*(randn(N/2,1) + 1i*randn(N/2,1))/sqrt(2);

n1, n2 and n3 have mean zero and variance no, This no is the $\sigma^2$ that we used in the equations.

6. Generate random message bits for users using the following command:

        x1 = randi([0 1],N,1);
        x2 = randi([0 1],N,1);
        x3 = randi([0 1],N,1);

7. Do QPSK modulation for each user's message. For this, we are going to use MATLAB's in-built QPSKModulator object. This will greatly simplify our modulation and demodulation part. First, we have to create the QPSKModulator and QPSKDemodulator object as follows:

        QPSKmod = comm.QPSKModulator('BitInput',true);       %Modulator object
        QPSKdemod = comm.QPSKDemodulator('BitOutput',true);  %Demodulator object

QPSKmod and QPSKdemod are our modulator and demodulator objects. We have set the argument 'BitInput' as true because we are going to feed raw binary data. 

Using our QPSKmod object to perform modulation is very simple. We use the step function and, in its argument, pass our QPSKmod object and the binary bit stream to be modulated.

        xmod1 = step(QPSKmod, x1);
        xmod2 = step(QPSKmod, x2);
        xmod3 = step(QPSKmod, x3);

8. Do superposition coding to create the NOMA transmit signal

        x = sqrt(a1)*xmod1 + sqrt(a2)*xmod2 + sqrt(a3)*xmod3;

9. Iterate over every value of transmit power: ('u' is used as the iteration variable) 

for u = 1:length(Pt)

        (i) Write received signal equation for all the three users

               y1 = sqrt(pt(u))*x.*h1 + n1;
               y2 = sqrt(pt(u))*x.*h2 + n2;
               y3 = sqrt(pt(u))*x.*h3 + n3;

        (ii) Perform equalization by dividing each received signal with the respective user's fading coefficient 

               eq1 = y1./h1;
               eq2 = y2./h2;
               eq3 = y3./h3;

        (iii) First, lets do the processing at the receiver side of U1. Directly demodulate eq1 to get x1. To do this, we use the QPSKDemodulator object we created as follows: 

                dec1 = step(QPSKdemod, eq1);

         (iv) Moving on to U2. First, directly decode x1 from eq2. 

                dec12 = step(QPSKdemod, eq2);

dec12 is in 0's and 1's. Before subtracting dec12 from eq2, we must first remodulate it to convert it to the same form as in eq2. So, let's do that.

                dec12_remod = step(QPSKmod, dec12);

Now, we can perform SIC to remove our estimate of U1's data (i.e., dec12_remod) from eq2, as shown:

                rem2 = eq2 - sqrt(a1*pt(u))*dec12_remod;

rem2 contains U2 and U3's data. Do direct QPSK demodulation on rem2 as before, to get U2's data.

        (v) Moving on to U3. First direct decode x1 from eq3. Remodulate the estimate of x1 that is obtained and subtract it from eq3.

               dec13 = step(QPSKdemod, eq3);
               dec13_remod = step(QPSKmod, dec13);
               rem31 = eq3 - sqrt(a1*pt(u))*dec12_remod;

 Again, demodulate rem31 to get x2. Remodulate the estimate of x2 and subtract it from rem31.

               dec23 = step(QPSKdemod, rem31);
               dec23_remod = step(QPSKmod, dec23);
               rem3 = rem31 - sqrt(a2*pt(u))*dec23_remod;               

               dec3 = step(QPSKdemod, rem3);    %Demodulate rem3 to get dec3

        (vi) BER calculation. For this, we use MATLAB's inbuilt biterr() function.

               ber1(u) = biterr(dec1, x1)/N;
               ber2(u) = biterr(dec2, x2)/N;
               ber3(u) = biterr(dec3, x3)/N;

end for loop.

        (vii) Plot the BER vs transmit power graphs of all the three users. We get a graph like this

We can see that the user 1 has the highest BER among the three. That is because he suffers the most interference. That is, both User 2 and User 3 cause interference for User 1. User 2 suffers moderate interference due to User 3. Finally, User 3 is free from interference and has the lowest BER in the group.

The BER performance is also strongly affected by the power allocation scheme that is used. Here, we have used fixed power allocation, which is not the best solution. If we resort to more sophisticated power allocation schemes, we may see further improvement in performance.