NOMA - How successive interference cancellation (SIC) works?

NOMA uses power domain multiplexing of users sharing same time and frequency resources. This is accomplished by performing superposition coding at the transmitter and successive interference cancellation (SIC) at the receiver. In the previous post, we saw a graphical view of superposition coding. In this post, we will see how SIC is carried out to decode the superposition coded signal at the receiver side.

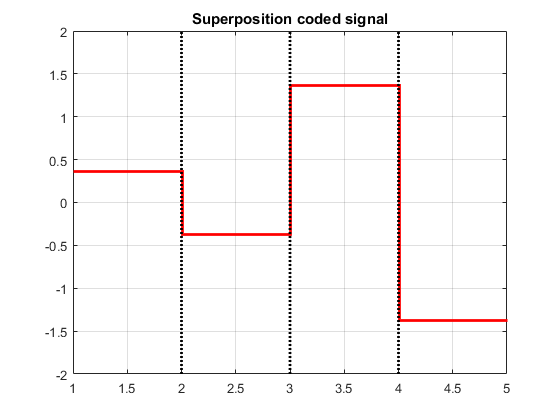
As a quick recap, we had two users with data x₁ and x₂ respectively. (What if we had more than two users?) We first did BPSK modulation to both x₁ and x₂. Then we obtained the superposition coded signal as x = √a₁x₁ + √a₂x₂ where, a₁ and a₂ are the power weights given to x₁ and x₂ respectively, such that, a₁ + a₂ = 1. We took an example of x₁ = 1010 and x₂ = 0110. After BPSK modulation and choosing a₁ = 0.75 and a₂ = 0.25, we obtained the superposition coded signal x, as shown below:

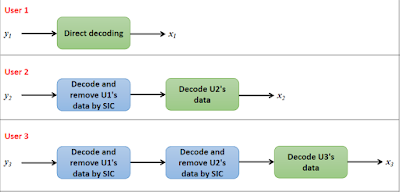
Before decoding, let us take a look at SIC algorithm. SIC is an iterative algorithm where data is decoded in the order of decreasing power levels. That is, data corresponding to the user who is given the highest power is decoded first, then the data of the user who is given the next highest power is decoded. This process repeats till we have decoded all user's data. For our simple case of two user NOMA system, the steps involved in SIC are described below:

• Step 1: Directly decode x to get the signal that is weighed with high power.
For example, if x₁ is given more weight, (i.e., a₁ > a₂), direct decoding of x gives x₁.
• Step 2: Multiply the signal decoded in step 1 by its corresponding weight and subtract it from x.
  For example, if x₁ is decoded in the previous step, subtract √a₁x₁ from x. This would give us, x - √a₁x₁.
• Step 3: Decode the signal obtained in step 2 to get the other signal which was multiplexed with low power.
  For example, decoding of x - √a₁x₁ obtained from the previous step would yield us x₂

These steps may appear pretty foggy, but please bear with me as we follow through our example to prove for ourselves that the SIC algorithm indeed works nicely.

Now, let's apply SIC to our example step by step. (Here, we've made a perfect SIC assumption. To see what happens when SIC is imperfect, see this post). Recall from the previous post that we chose values for power weights as a₁ = 0.75 and a₂ = 0.25. This means that we have given x₁ more power weight that x₂. So, following step 1, when we do direct decoding of x, we would get x₁.

What do we mean by direct decoding? In our case, we have used BPSK modulation at the transmitter side. So what we mean by direct decoding is that, we are going to apply BPSK demodulation directly to x.

We might think that we would run into trouble because know that x contains a linear combination of x₁ and x₂, which are two different messages. But we will see shortly that SIC handles this problem very nicely. So let's go ahead and perform BPSK demodulation on x.

BPSK demodulation is basically, a simple thresholding. Let's set the threshold to zero. For each symbol, if the amplitude exceeds zero, we are going to decode it as 1, and 0 otherwise.

This is a plot of x, and the threshold is denoted as a solid black horizontal line. Let's decode x symbol by symbol. We observe that the first and third symbols lie above the threshold of zero. So, we make the decision that the first and third transmitted bits are ones. The second and fourth symbols lie below the threshold. So, we make the decision that the second and fourth transmitted bits are zeros. Thus, the decoded sequence in order is 1010. Which is the same as x₁!

In other words, we arrived at x₁ by directly performing BPSK demodulation on x, totally ignoring the fact that x had a component of x₂ too. This was possible because, we allocated a higher power weight to the x₁ component of x. Thus the presence of the other component x₂ in x can be safely ignored. In other words, we treat x₂ as interference and ignore it.

We've completed step 1 of SIC process. What is the intuition behind the next two steps of SIC?
We know x = √a₁x₁ + √a₂x₂. The values of √a₁ and √a₂ are known to as because they are design choices. Further, we obtained x₁ by following step 1. So if we subtract √a₁x₁ from x, we will be left with √a₂x₂. From √a₂x₂, it is pretty much easy to obtain x₂.

Let's move on to step 2.We have to multiply the x₁ component by its corresponding power weight and subtract it from x. We have to be careful now. We have obtained x₁ to be 1010. But x₁ is present in x in its BPSK modulated form. In other words, x does not contain x₁ as 1010. x contains x₁ as 1 -1 1 -1, which is the BPSK modulated version of 1010. So, we have to subtract this BPSK modulated version of x₁ component from x. After subtraction, the graph would look like this.

Notice that this looks similar to the graph which shows scaled data of user 2 in the previous post.

We are done with step 2. Moving on to step 3. After subtraction, we simply have to demodulate the resulting signal using BPSK rule as before. Following BPSK rule, we see that the first and fourth symbol would be demodulated as zeros and the other symbols would be demodulated as ones. Thus, the demodulated signal, put in order is 0110, which is same as x₂.

This and the previous post are written just to prove for ourselves that NOMA indeed works as intended. We have successfully multiplexed two separate data in the power domain and recovered it. We have considered a perfectly ideal case by not including channel noise effects etc., Our goal here is just to understand how NOMA works. We will see the BER performance of NOMA in the presence of AWGN in the following posts. Thank you.

PS: Click here to download the complete MATLAB code for NOMA with superposition coding and SIC.
This is just a toy example to understand the concept of NOMA. In the next post, we will see how to simulate a NOMA system and plot its bit error rate (BER) using MATLAB.

Reference:
This is an excellent paper which explains the basics of NOMA for starters.
Y. Saito et al., Non‐orthogonal multiple access (NOMA) for cellular future radio access, IEEE 77th Vehicular Technology Conference (VTC Spring) (Dresden, Germany), 2013, pp. 1-5.

Next post: How to simulate a simple NOMA system using MATLAB