NOMA - How superposition coding works?

Non Orthogonal Multiple Access (NOMA) is a candidate multiple access scheme for 5G. The fact that NOMA allows multiple users to transmit and receive simultaneously using the same frequency may appear intriguing. The two key operations that make NOMA possible are superposition coding which must be done at the transmitter side and successive interference cancellation (also known as SIC) at the receiver side. In this post we will see about superposition coding.

Let us say two users User 1 and User 2 are going to communicate simultaneously using the same frequency. Let x₁ denote User 1's data and x₂ denote User 2's data. For simplicity, let us assume that each user has just 4 bits of data to send. This assumption is far from reality, but is sufficient to understand the basic working of NOMA.

Let x₁ = 1010 and x₂ = 0110. A graphical view of x₁ and x₂ is shown below.

x₁ and x₂ must undergo digital modulation before transmission. Let's use BPSK for simplicity. BPSK maps 0's to -1's and 1's to +1's. After BPSK modulation, x₁ is mapped to +1 -1 +1 -1 and x₂ is mapped to -1 +1 +1 -1 as shown below.

NOMA requires superposition coding at the transmitter side. Superposition coding is a fancy term for power domain multiplexing. To superpose means to add. So basically we're going to add x₁ and x₂ together. But before doing that, we are going to multiply them with different power levels. Then, we will add them together.

From the previous figure, we can see that both x₁ and x₂ have a peak amplitude of ±1. That means, they both have unit power or, 1 watt (Remember, power = amplitude²).

Lets say we give the power weights as a₁=0.75 to user 1 and a₂=0.25 to user 2. A rule to follow here is that a₁ and a₂ must sum up to 1.
Here, we have used fixed power allocation. That is fixed values of a₁ and a₂. To know how to optimize a₁ and a₁, see this post: How to do power allocation in NOMA?
First, let's scale x₁ and x₂ with √a₁ and √a₂ respectively. Why square root? Because a₁ and a₂ represent the power scaling factors. To make them represent amplitude, we take the square root. After scaling, the signals look as shown below. Note that the amplitude of x₁ is scaled to √a₁ = √0.75 = 0.866 and the amplitude of x₂ is scaled to √a₂ = √0.25 = 0.5. So our amplitude scaled versions of the data are, √a₁x₁ = 0.866 -0.866 0.866 -0.866 and √a₂x₂ = -0.5 0.5 0.5 -0.5.

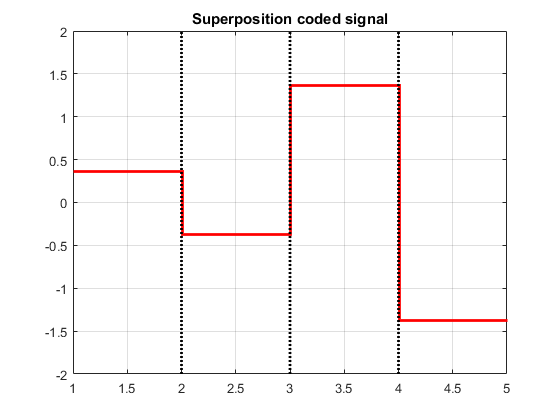
Now it is time to add both the scaled signals together. The resulting signal is called superposition coded signal and is denoted by,
x = √a₁x₁ + √a₂x₂. Adding them both together we get x = 0.366 -0.366 1.366 -1.366.
A graphical representation of x is shown below. Note that each corresponding term of √a₁x₁ and √a₂x₂ from the previous figure are added together to get the graph of x shown below.

This signal x is the superposition coded NOMA signal that is actually transmitted into the channel. So, that's how superposition coding is done. Note that x is a linear combination of x₁ and x₂. In the next post, we shall see how we can recover x₁ and x₂ from x using successive interference cancellation (SIC).

PS: Click here to download the MATLAB code for superposition coding. Try different values for data x₁, x₂ and power weights a₁ and a₂ to gain an intuition on how superposition coding works!