Single Carrier NOMA (SC NOMA) - How many users can it support?

We saw how non-orthogonal multiple access (NOMA) can somehow magically break the capacity limitation faced by the other traditional orthogonal multiple access (OMA) schemes. OMA schemes like TDMA, FDMA, CDMA, OFDMA separates the users in time, frequency, code, subcarrier domains respectively. No two users are allowed to share the same resource simultaneously. If this condition is violated, interference would occur and both users would lose their data.

For a moment, let's consider an OFDMA network with 64 subcarriers. If we assign one orthogonal subcarrier per user, the maximum number of users we can simultaneously serve is 64. If the 65th user requests a connection, his call must be dropped or he must wait for one of the other users to finish transmitting. This is because we don't have any more orthogonal subcarrier to assign to the new user. This orthogonality bottleneck imposes a capacity limitation on the number of users who can simultaneously access the OMA network. 

NOMA breaks this capacity bottleneck by allowing simultaneous transmission of multiple users in the same frequency carrier. Of course, interference would occur. But NOMA employs a technique called successive interference cancellation (SIC) to intelligently remove the interference.

Till now, we saw about two user NOMA and three user NOMA simulation. After reading those posts, some of our readers pointed out to me, the next important question that arises. How many users can I multiplex in the same carrier? Can I multiplex 100 users? Won't this make the receiver side processing complicated? These are interesting questions and we will seek to find their answers in this post.

SIC complexity at strong users

We know that, while performing superposition coding at the transmitter side, the users are ordered according to their channel conditions and the weakest user is allocated the most power. For example, if we have $K$ users, and if they are ordered such that, $|h_1|^2 \lt |h_2|^2 \lt ... \lt |h_K|^2$, then their corresponding power allocation coefficients will be ordered as $\alpha_1 \gt \alpha_2 \gt ... \alpha_K$.

While doing this power allocation, we should ensure that, $\alpha_1 \gt \alpha_2 + \alpha_3 + ... \alpha_K$ and $\alpha_2 \gt \alpha_3 + \alpha_4 + ... \alpha_K$, $\alpha_3 \gt \alpha_4 +  ... \alpha_K$ and so on.

At the receiver side, the weakest user, i.e., $U_1$, will perform direct decoding. Since, $\alpha_1 \gt \alpha_2 + \alpha_3 + ... \alpha_K$, all other users' data are considered interference. So, $U_1$ does not have any complex processing involved. OK. Let's move on to $U_2$.

In the received signal of $U_2$, $U_1$'s data will be dominating because,  $\alpha_1 \gt \alpha_2 + \alpha_3 + ... \alpha_K$. So, $U_2$ has to first perform SIC to estimate and remove $U_1$'s data. Once $U_1$'s data is removed, we will have, $\alpha_2 \gt \alpha_3 \gt \alpha_4 \gt ... \alpha_K$. So now, $U_2$'s data is dominating. Therefore, $U_2$ can perform direct decoding, by treating the data of users $U_2$, $U_3$, ... as interference.

In a similar fashion, $U_3$ must perform SIC to remove $U_1$ and $U_2$'s data before decoding its own signal. $U_4$ must remove $U_1$, $U_2$, and $U_3$'s data before decoding its own signal. Following the same train of thought, how much times should the strongest user ($U_K$) perform SIC before decoding his own data? $K-1$ times. He must remove every single users' data from his received signal. Only then $\alpha_K$ will be dominating.

Thus, if we multiplex 100 users in the same carrier, the 100th user must perform SIC 99 times before decoding his own data. This is not only computationally complex, but also consumes much time leading to processing delay.

As if this processing itself is not complicated enough, a new problem called SIC error propagation will also occur. For example, $U_5$ must perform SIC for $U_1$ , $U_2$, ... $U_4$'s data. If $U_1$'s data is decoded in error, then this will lead to a wrong signal being subtracted in the SIC process, which would lead to decoding of $U_2$'s data erroneously and this error propagates on and on to the decoding of $U_5$ own data.

But this is not the only problem with multiplexing large number of users in the same carrier.

The problem of Interference at weak users

Again, let's assume we have $K$ users, with $U_1$ as the weakest user and $U_K$ as the strongest user. $U_K$ already has the problem of complicated and time consuming signal processing requirement. Now, the problem with $U_1$ is this: $U_1$ does direct decoding treating all other users' data as interference. So, the achievable rate equation of $U_1$ will have $K-1$ interference terms. It will look like this:$$R_1 = log_2\left(1 + \dfrac{\alpha_1P|h_1|^2}{\left(\alpha_2 + \alpha_3 + ... \alpha_K\right)P|h_1|^2 + \sigma^2}\right)$$

In the same way, the achievable rate equation of $U_2$ will be: $$R_2 = log_2\left(1 + \dfrac{\alpha_2P|h_2|^2}{\left(\alpha_3 + \alpha_4 + ... \alpha_K\right)P|h_2|^2 + \sigma^2}\right)$$

We can already see the problem. The amount of interference faced by the users is higher when more users are multiplexed in the same carrier.

The problem of power allocation

When we had two users, we arbitrarily chose $\alpha_1$ to be some value, say 0.75, and $\alpha_2 = 0.25$. By doing this, we were able to easily satisfy the conditions $\alpha_1 \gt \alpha_2$ and $\alpha_1+\alpha_2=1$. When we had three users, in this post, we choose, $\alpha_1 = 0.85$, $\alpha_2=0.15$ and $\alpha_3=0.05$. Thus satisfying,

• $\alpha_1 \gt \alpha_2 \gt \alpha_3$
• $\alpha_1 \gt \alpha_2 + \alpha_3$
• $\alpha_2 \gt \alpha_3$
and
• $\alpha_1 + \alpha_2 + \alpha_3 = 1$
.

When we have $K$ users, we have even more conditions to satisfy.

• $\alpha_1 \gt \alpha_2 \gt \alpha_3 \gt ... \gt \alpha_K$
• $\alpha_1 \gt \alpha_2 + \alpha_3 + ... + \alpha_K$
• $\alpha_2 \gt \alpha_3 + \alpha_4 +... + \alpha_K$
...
• $\alpha_{m} \gt \alpha_{m+1}+\alpha_{m+2}+...\alpha_{K}$
and
• $\alpha_1 + \alpha_2 + ... + \alpha_K = 1$

How do we pick $\alpha_1, \alpha_2, ... \alpha_K$ to satisfy all these conditions? Obviously, it is quite complicated to pick them by trial and error. So, let's see a power allocation method to tackle this problem.

A power allocation method for multiple user single carrier NOMA

First, pick fraction less than 1. For example, $\dfrac{3}{4}$ or $\dfrac{2}{5}$ etc. Let's pick $\dfrac{3}{4}$. Start with the weakest user. For U1, set $\alpha_1=\dfrac{3}{4}$. 

• If $K=2$, set $\alpha_2 = 1 - \alpha_1$. Otherwise, set $\alpha_2 = \dfrac{3}{4}(1 - \alpha_1)$. 
• If $K = 3$, set  $\alpha_3 = 1 -(\alpha_1+\alpha_2)$. Otherwise, set $\alpha_3 = \dfrac{3}{4}\left(1 - (\alpha_1+\alpha_2)\right)$.
• If $K = 4$, set  $\alpha_4 = 1 -(\alpha_1+\alpha_2+\alpha_3)$. Otherwise, set $\alpha_4 = \dfrac{3}{4}\left(1 - (\alpha_1+\alpha_2+\alpha_4)\right)$.
• ...
• If $K = m$, set  $\alpha_m = 1 -(\alpha_1+\alpha_2+...+\alpha_{m-1})$. Otherwise, set $\alpha_m = \dfrac{3}{4}\left(1 - (\alpha_1+\alpha_2+...\alpha_{m-1})\right)$.

By following this heuristic repeatedly to all the users, we will arrive at a power allocation solution which satisfies all the conditions mentioned in the previous section. 

Although this algorithm guarantees proper power allocation in terms of meeting the required conditions, we can immediately see a new problem arising: As more and more users are squeezed into the network, the strongest user will be allocated less and less power. This will lead to a decrease in his achievable data rate.

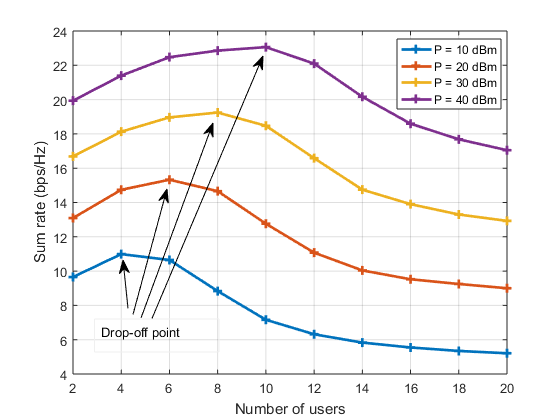
Now that we have seen some of the problems faced by what we call single carrier NOMA (or SC-NOMA), let's do a MATLAB simulation to see all these problems in effect. Let's plot the achievable sum rate of an SC-NOMA network by varying the number of multiplexed users. We will get a graph like this.

Download the MATLAB code here

What can we infer from this graph?

• As the number of users of SC-NOMA is increased, the sum capacity of the network initially increases and then drops and saturates. 
• This initial increase is due to the same reasons that NOMA offers better capacity than OMA. The interference levels are manageable and the strongest user, although he is allocated the least power, is given a respectable amount of power.
• We can observe a drop off point beyond which the capacity falls. This drop off point can be regarded as the maximum limit on the number of users who can be admitted into the network without any performance degradation.
• The drop off point moves towards the right as the transmit power is increased. That is, When 10dBm transmit power was used, the sum rate started to decrease beyond 4 users. But when 40dBm transmit power was used, the drop off point was beyond 10 users. This behavior is mainly due to the power allocation strategy that we adopted. The weakest user will be assigned the least fraction of power and a small fraction of 40 dBm is greater than a small fraction of 10 dBm.
• Thus, to accommodate more users without performance degradation, we must increase the transmit power. 

Conclusion

From our simulation, we found that we cannot keep on increasing the number of users multiplexed in the same carrier. So, to answer our initial questions, multiplexing 100 users in the same carrier will pose more problems in terms of SIC computational complexity, delay, power allocation computation and reduction in achievable rate. The upper limit on the number of users is determined by the drop off point in our graph. If so, what can we do to accommodate all the 100 users in the same carrier? We can go for hybrid NOMA techniques which combine OMA and NOMA concepts together. We will see more about them in the future posts. Thank you.