Does power allocation affect NOMA?

-

Next post: How does user cooperation help NOMA?

Till now, we simulated various performance parameters like bit error rate (BER), capacity and outage probability of NOMA by using fixed power allocation method. By fixed power allocation, we mean that regardless of the channel condition, we always set $\alpha_1 = 0.75$ (for far user) and $\alpha_2 = 0.25$ (for near user). This is one way to allocate power. And the advantages of this fixed power allocation method are:

  • No computation required
  • No knowledge of channel state information (CSI) is required

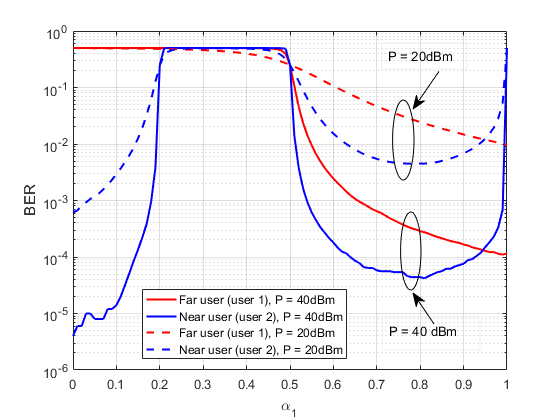
But this is not the optimum way to allocate power. If we write a simple MATLAB code to plot the BER as a function of power allocation coefficients, we get a plot like this: (Download the code here)

Some notes about this plot

  • In this plot, we consider user 1 to be the far user and user 2 to be the near user.
  • Also, we have used fixed power allocation method. That is, we did not alter the coefficients based on channel conditions. We have just plotted the BERs when we fix different values of power allocation coefficients.
  • The solid lines are for a transmit power of 40 dBm and the dotted lines are for 20 dBm.
  • The above plot can be interpreted in terms of $\alpha_2$ by doing the transformation $\alpha_2 = 1 - \alpha_1$. (since, we know that, $\alpha_1 \gt \alpha_2$ and, $\alpha_1 + \alpha_2 =1$)

What can we infer from this plot?

  • Firstly, we see that some values of power allocation coefficients are better than others. That is the BER is low for some values of $\alpha_1$ and high for other values.
  • The near user (user 2) experiences low BER ($\lt10^{-4}$) at two regions of this plot. i.e., around $\alpha_1 < 0.1$ (in other words, $\alpha_2 \gt 0.9$) and around $\alpha_1 \approx 0.8$ (in other words, $\alpha_2 \approx 0.2$).


  • The BER for near user (user 2) is lower when $\alpha_1 < 0.1$ ($\alpha_2 \gt 0.9$) than when $\alpha_1 \approx 0.8$ ($\alpha_2 \approx 0.2$). So, can we choose $\alpha_1 < 0.1$ and $\alpha_2 \gt 0.9$)? No. Because the far user (user 1) has very high BER in this regime


  • If we want both users to fairly benefit from NOMA, the ideal regime to operate is $\alpha_1\in[0.5,1]$, $\alpha_2\in[0,0.5]$.


  • Towards the left end of the plot, $\alpha_1 \approx 0$ and $\alpha_2 \approx 1$. This means a very large power is allocated to the near user (user 2). Therefore, he has a very low BER.


  • As $\alpha_1 \approx 0$ and $\alpha_2 \approx 1$, the near user's (user 2) data is dominating and hence, the far user (user 1) will not be able to directly decode his signal. This explains his high BER.


  • Towards the right end of the plot, $\alpha_1 \approx 1$ and $\alpha_2 \approx 0$. This means a very large power is allocated to the far user (user 1). Therefore, he has a decreasing BER trend.


  • As $\alpha_1 \approx 1$, the interference from the high power far user (user 1) data is so large that the near user (user 2) suffers high BER.


In our next post, we will see some ways to optimize the power allocation coefficients based on the knowledge of instantaneous channel state information (CSI). Thank you!

Next post:
How to do power allocation in NOMA?

Comments

  1. Satarupa11 June 2020 at 05:04

    thank you... Kindly share a post on uplink too...

    ReplyDelete
    Replies
    1. Joe11 June 2020 at 06:24

      Hi Satarupa,
      Thanks for your suggestion. Will make a post on that!

      Delete
  2. Med18 June 2020 at 13:19

    Hello ! Can you explain this line to me: eq1 = y1./h1 ;
    what this is all about and why you divided on y
    thank you in advance!!

    ReplyDelete
    Replies
    1. Joe18 June 2020 at 13:51

      Hi, due to fading, the transmitted signal, x, undergoes random amplitude and phase fluctuations. We model this effect by multiplying x with the Rayleigh fading coefficient, h.

      So, the received signal is of the form, y = hx + n. Fading is undesirable and the effect of h must be removed from the received signal y.

      If we have perfect knowlegde of h, the effect of fading can be undone by dividing y by h.

      Hope this helps

      Delete
  3. Med19 June 2020 at 02:12

    Yes yes Thank you very much!

    ReplyDelete
  4. Mariam26 June 2020 at 17:06

    Hi! Do you have a matlab code for BER vs SNR plot for power domain ?

    ReplyDelete
    Replies
    1. Joe27 June 2020 at 01:36

      Hi Mariam, BER vs SNR of power domain NOMA in AWGN channel is explained in this post https://ecewireless.blogspot.com/2020/04/simulation-of-ber-of-non-orthogonal.html

      Delete
  5. Unknown30 June 2020 at 23:10

    Hi Joe,
    When we allocating power to far users [0.2: 0.5] and similarly for nearby users is [0.8: 0.5]?
    Why are the two users still subjected to such a high BER?
    Thank you!

    ReplyDelete
    Replies
    1. Joe1 July 2020 at 02:15

      Hi, we know that in the SINR expression of far user, a1 appears in the numerator and a2 appears in the denominator. So whenever a2 > a1, (in the range mentioned by you,) the interference term in the denominator would dominate, leading to high BER.

      Delete
    2. Unknown2 July 2020 at 05:16

      Can you distinguish SINR and SNR?
      Thank you!

      Delete
    3. Joe2 July 2020 at 10:28

      SNR = sigPower/noisePower as in the equation of near user after SIC

      SINR = sigPower/(interferencePower + noisePower) as in the equation of far user, and near user before SIC

      Delete
  6. Abdelrahim22 December 2020 at 10:37

    thanks alot

    can u please contact with me As soon as possible on
    abdelrahimjomaa2@gmail.com

    ReplyDelete
    Replies
    1. Joe22 December 2020 at 20:36

      Sure, you can ping me at electronicswithme@gmail.com

      Delete
  7. Unknown12 October 2021 at 04:35

    Hi ,thanks for sharing this i am referring your blog and at this very initial level of research in the field of power allocation its very helpful for me. Can you Please suggest any resources for the same where i could learn basics for this

    ReplyDelete
  8. Lina15 November 2021 at 08:01

    Hi JOE,
    I am trying to find the effect of power coefficients on MIMO-NOMA but something wrong ,could you please check my code ?

    N = 5*10^5;
    Pt = 20;
    No = -114;

    pt = (10^-3)*db2pow(Pt);
    no = (10^-3)*db2pow(No);

    a1 = 0:0.01:1; %power coffiecent
    a2 = 1 - a1;

    % distance
    d1 = 1000; d2 = 500;

    %path loss exponent
    eta = 4;

    %Rayleigh fading channels for MIMO-NOMA & MIMO-OMA
    h11 = sqrt(d1^-eta)*(randn(N,1) + 1i*randn(N,1))/sqrt(2);
    h12 = sqrt(d1^-eta)*(randn(N,1) + 1i*randn(N,1))/sqrt(2);
    h21 = sqrt(d2^-eta)*(randn(N,1) + 1i*randn(N,1))/sqrt(2);
    h22 = sqrt(d2^-eta)*(randn(N,1) + 1i*randn(N,1))/sqrt(2);

    h1 = h11+h12;
    h2 = h21+h22;

    %Channel gains
    g1 = (abs(h1)).^2;
    g2 = (abs(h2)).^2;


    %Generate noise samples for both users
    w1 = sqrt(no)*(randn(1,N)+1i*randn(1,N))/sqrt(2);
    w2 = sqrt(no)*(randn(1,N)+1i*randn(1,N))/sqrt(2);


    data1 = randi([0 1],1,N);
    data2 = randi([0 1],1,N);

    x1 = 2*data1 - 1;
    x2 = 2*data2 - 1;

    for u = 1:length(a1)

    %transmited info for NOMA ,MIMO-NOMA
    x = sqrt(pt)*(sqrt(a1(u))*x1 + sqrt(a2(u))*x2);

    %------------


    %FOR MIMO-NOMA
    ym1 = x.*h1 + w1;
    ym2 = x.*h2 + w2;



    %----------


    %Equalize for MIMO-NOMA
    eqm1 = ym1./h1;
    eqm2 = ym1./h2;


    %DECODING FOR MIMO-NOMA MIMO-NOMAAAAAAAA MIMO-NOMAAAAA
    %AT USER1-------
    %Direct decoding of x1 from ym1
    xm1_hat = zeros(1,N);
    xm1_hat(eqm1>0) = 1;

    %Compare decoded xm1_hat with data1 to estimate BER
    berm1(u) = biterr(data1,xm1_hat)/N;
    %----------------------------------


    %AT USER 2-------------------------
    %Direct decoding of x1 from ym2
    xm12_hat = ones(1,N);
    xm12_hat(eqm2<0) = -1;

    ym2_dash = eqm2 - sqrt(a1(u)*pt)*xm12_hat;
    xm2_hat = zeros(1,N);
    xm2_hat(real(ym2_dash)>0) = 1;

    berm2(u) = biterr(xm2_hat, data2)/N;

    end





    %FIGURE FOR MIMO-NOMA MIMO-NOMA MIMO-NOMAAA

    semilogy(a1, berm1,'-*r', 'linewidth',1.5); hold on; grid on;
    semilogy(a1, berm2,'-sr', 'linewidth',1.5);
    xlabel('\alpha_1');
    ylabel('BER');

    legend('MIMO-NMA Far user','MIMO-NOMA Near user');
    ---------------
    it says that the matrix is very big, how can I overcome this problem?
    TAHNK YOU in advance ^^

    ReplyDelete
    Replies
    1. Ameer Saeed Mohammed Ali26 January 2022 at 11:09

      If you wont do this code for more two user . How can you set this lines a1 = 0:0.01:1; %power coffiecent
      a2 = 1 - a1;

      Delete
    2. Ameer Saeed Mohammed Ali26 January 2022 at 11:11

      can you give this code but for three users
      ameersaeed469@gmail.com

      Delete

Post a Comment

Popular posts from this blog

How to simulate BER, capacity and outage probability of NOMA (Rayleigh fading) using MATLAB?

-
Image
Simulation of BER of Non orthogonal multiple access (NOMA) in Rayleigh fading channel - MATLAB code with explanation Next post: What happens when SIC is imperfect? In the previous post , we saw how to simulate a simple two user NOMA network over an AWGN channel in MATLAB. We also plotted the BER vs SNR graphs of both the users and observed the waterfall trend. The AWGN assumption simplified the channel model and allowed us to learn the basic skeletal operation of NOMA. In this post, we will use MATLAB to simulate the capacity, outage and BER performance of a two user NOMA network by following a more realistic model namely, Rayleigh fading model. The MATLAB code to plot BER, capacity and outage probability of NOMA are also available for download in this page . So, let's get started! Wireless channel is prone to multipath propagation and fading. Several channel models are available to capture the effects of fading. Each model deals with a particular scenario....
Read more

How to simulate a simple NOMA system (AWGN) using MATLAB?

-
Image
Simulation of BER of Non orthogonal multiple access (NOMA) in AWGN channel - MATLAB code with explanation You can download the MATLAB code directly here . In the previous two posts, we took a toy example to understand the concept of NOMA and to prove to ourselves that NOMA indeed works as expected. As we said before, NOMA uses superposition coding at the transmitter end and successive interference cancellation at the receiver end. In this post, we will see how to simulate a simple two user NOMA system using MATLAB. We will be plotting the BER performance of NOMA in an additive white gaussian noise (AWGN) channel. The AWGN assumption here is made to keep things simple so that we can pay more attention to the actual skeleton of NOMA implementation. We will improve on this model and do the similar exercise over a Rayleigh fading channel in the next post . The MATLAB code used in this example is available for download here . See this post on How to do power allocation i...
Read more

How to do power allocation in NOMA? (with fairness to far/weak user)

-
Image
Next post: NOMA with more than two users Power allocation is very important in non orthogonal multiple access (NOMA). In the previous post " Does power allocation affect NOMA? ", we saw how the bit error rate (BER) of NOMA has a strong relationship with the values of power allocation coefficients. We used fixed power allocation till now. That is, we fixed the values of $\alpha_1$ and $\alpha_2$ irrespective of the channel conditions. But there are better ways to optimize $\alpha_1$ and $\alpha_2$ dynamically based on the values of channel state information (CSI).  There are a few different dynamic power allocation schemes each trying to accomplish a specific goal. The goal could be maximizing the sum rate, maximizing the energy efficiency, etc., The power allocation scheme we are going to see in this post is a simple one whose goal is to provide user fairness. Let's call this fair power allocation ...
Read more