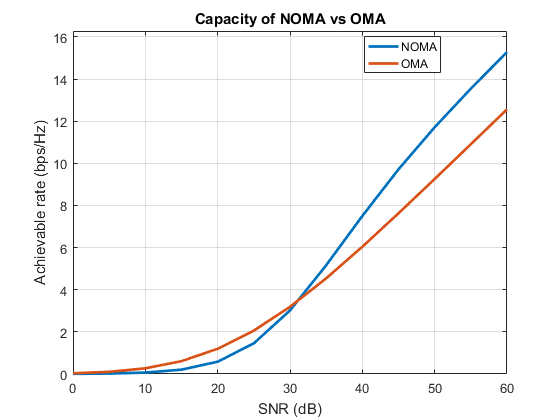
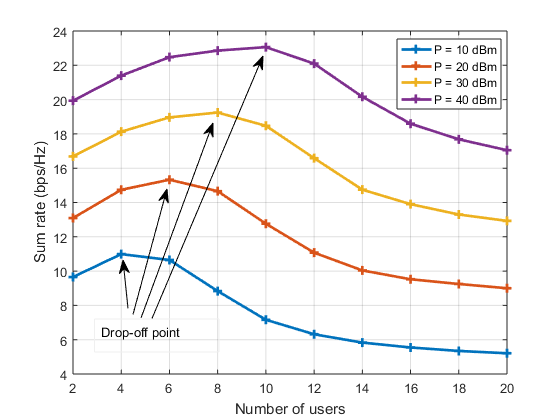
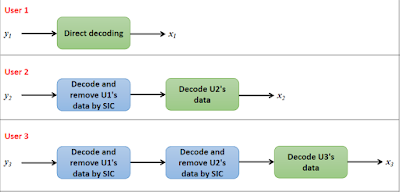
Uplink NOMA - Outage Probability in MATLAB

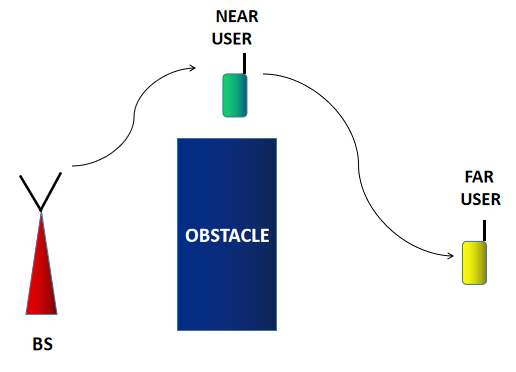
Till now, we were dealing with downlink NOMA (where the base station (BS) transmits NOMA signal to the end users). In this post, let's see how to perform NOMA in the uplink. Uplink communication is when the users transmit to the BS. Download the MATLAB code here Network model Let's consider the following network consisting of two users, who want to transmit their data to the BS. Fig. 1: Uplink NOMA network model In this example, we are taking $U_f$ as the far user and $U_n$ as the near user. Let $d_f$ and $d_n$ denote their distances from the BS. $h_f$ and $h_n$ represent their corresponding Rayleigh fading coefficients. ($d_f \gt d_n$ and $|h_f|^2 \lt |h_n|^2$) How to do power domain multiplexing in uplink NOMA? The power domain multiplexing part is done in a slightly different way for uplink NOMA. As we know, in downlink NOMA, the BS used superposition coding to perform power domain multiplexing. But in u...