NOMA vs OMA - Capacity comparison

As a candidate multiple access technology for 5G, non-orthogonal multiple access (NOMA) offers greater transmission capacity than current orthogonal multiple access (OMA) techniques. This increase in achievable rate is possible because NOMA allows simultaneous transmission of multiple user data in the same frequency carrier.

At the transmitter end, the users are multiplexed in the power domain by using superposition coding. At the receiver end, successive interference cancellation (SIC) is carried out to remove interference and to separate the individual user messages.

In this post, we will compare the achievable rate offered by NOMA and OMA schemes.

Download the MATLAB code here

System model

Let's consider a downlink communication scenario with a base station (BS) and $N$ users. Let $h_i$, denote the channel from the BS to the $i^{th}$ user. There are $N$ such channels, $h_1$, $h_2$, ... $h_N$.

Let us assume that user 1, with channel $h_1$ is farthest from the BS and hence, the weakest user. User 2 is the next and so on. User $N$ is the nearest/strongest user. This means the channel conditions of the users are arranged as follows: $|h_1|^2 < |h_2|^2 < ... |h_N|^2$

Signal model for NOMA

Let $x_1$, $x_2$, ... $x_N$ denote the messages to be transmitted to the users. The BS performs superposition coding with these messages and transmits the following NOMA signal into the channel: $$x_{NOMA} = \sqrt{P}\left(\sqrt{\alpha_1}x_1 + \sqrt{\alpha_2}x_2 + ... \sqrt{\alpha_N}x_N\right)$$

(1)

where $P$ is the total transmit power. $\alpha_1$ ... $\alpha_N$ represent the power allocation coefficients. Since the channels are ordered as $|h_1|^2 < |h_2|^2 < ... |h_N|^2$, the power allocation coefficients must be ordered as $\alpha_1 > \alpha_2 > ... \alpha_N$

We can represent $x_{NOMA}$ concisely as follows: $$x_{NOMA} = \sqrt{P}\sum_{i=1}^{N}\sqrt{\alpha_i}x_i$$

(2)

The received signal at user $i$ is given by, $$y_{i,NOMA} = x_{NOMA}h_i + w_i$$ 

(3)

where $w_i$ is the AWGN with zero mean and variance = $\sigma^2$.

Substituting for $x_{NOMA}$ from (1), we get, $$y_{i,NOMA} = \sqrt{P}\left(\sqrt{\alpha_1}x_1 + \sqrt{\alpha_2}x_2 + ... \sqrt{\alpha_N}x_N\right)h_i + w_i$$

(4)

Let's examine how (4) will look like for user 1 (the farthest user).

$$y_{1,NOMA} = \sqrt{P}\left(\underbrace{\sqrt{\alpha_1}x_1}_\textrm{desired and dominating} + \underbrace{\sqrt{\alpha_2}x_2 + ... +\sqrt{\alpha_N}x_N}_\textrm{interference}\right)h_1+ w_1$$

(5)

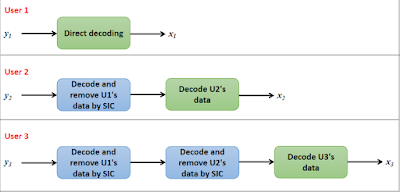
What is the decoding rule for user 1?

    Since user 1 is allocated the highest amount of power, the message intended for him will be dominating in the received signal. So, he just performs direct decoding, treating the messages intended for all other users as interference. Thus, the SINR for decoding user 1's signal is given by, $$\gamma_{1,NOMA}= \dfrac{\alpha_1P|h_1|^2}{\alpha_2P|h_1|^2+\alpha_3P|h_1|^2+...+\alpha_NP|h_1|^2+\sigma^2}$$

(6)

Next, let's look at user 2's received signal,

$$y_{2,NOMA} = \sqrt{P}\left(\underbrace{\sqrt{\alpha_1}x_1}_\textrm{undesired but dominating} + \underbrace{\sqrt{\alpha_2}x_2}_\textrm{desired}+\underbrace{  ... \sqrt{\alpha_N}x_N}_\textrm{interference}\right)h_2 + w_2$$

(7)

What is the decoding rule for user 2?

    Since the user 1 is allocated the highest power, his message will be dominating the received signal of all the other users. So, first user 2 should directly decode user 1's message, then perform SIC to remove it from $y_{2,NOMA}$. If the SIC operation is perfect, the resulting signal would be, $$y'_{2,NOMA} = \sqrt{P}\left( \underbrace{\sqrt{\alpha_2}x_2}_\textrm{desired and dominating}+ \underbrace{ ... \sqrt{\alpha_N}x_N}_\textrm{interference}\right)h_2 + w_2$$

(8)

After SIC, user 2's required message is the dominating term. So, now user 2 can directly decode his message from $y'_{2,NOMA}$ by treating all the remaining users' messages as interference. Thus, the SINR at user 2 to decode his own message is given by, $$\gamma_{2,NOMA} = \dfrac{\alpha_2P|h_2|^2}{\alpha_3P|h_2|^2+...+\alpha_NP|h_2|^2+\sigma^2}$$

(9)

We can extend the same thought process to obtain the decoding rule for users 3, 4 and so on. For example, user 3 has to first decode user 1's signal, perform SIC to eliminate it, then decode user 2's signal, perform SIC again, and then decode his own signal.

In general, for any user $i$, the SINR to decode his own signal is given by, $$\gamma_{i,NOMA} = \dfrac{\alpha_iP|h_i|^2}{\alpha_{i+1}P|h_{i}|^2+...+\alpha_NP|h_i|^2+\sigma^2}$$ 

(10)

This expression can be concisely written as, $$\gamma_{i,NOMA} = \dfrac{\alpha_iP|h_i|^2}{\sum_{j=i+1}^{N}\alpha_jP|h_i|^2 +\sigma^2}$$ 

(11)

The achievable rate for any general user $i$ can be written as, $$R_{i,NOMA} = log_2(1 + \gamma_{i,NOMA})$$

(12)

Finally, the sum rate of all the NOMA users is given by, $$R_{NOMA} = \sum_{i=1}^{N}R_{i,NOMA}$$

(13)

Signal model for OMA

Next, let's take a look at normal OMA transmission, As an example, let's consider TDMA. To serve $N$ users, TDMA requires $N$ time slots. In the first time slot, user 1's signal is transmitted, in the second time slot, user 2's signal is transmitted and so on. Also, let's assume that all the time slots are of equal duration. Let's say, in the $i^{th}$ time slot, user $i$'s signal is transmitted. Then, the transmit signal is given by, $$x_{i,OMA} = \sqrt{P}x_i$$

(14)

Comparing equations (1) and (13), we see that NOMA has the advantage of simultaneous transmission with controllable interference, while OMA users enjoy interference-free reception. The received signal at user $i$ will be, $$y_{i,OMA} = \sqrt{P}x_ih_i + w_i$$

(15)

Now, the SNR of the $i^{th}$ OMA user is given by, $$\gamma_{i,OMA} = \dfrac{P|h_i|^2}{\sigma^2}$$

(16)

The achievable rate for the $i^{th}$ OMA user is given by, $$R_{i,OMA} = \dfrac{1}{N}log_2(1 + \gamma_{i,OMA})$$

(17)

Finally, the sum rate of OMA is given by, $$R_{OMA} = \sum_{i=1}^{N}R_{i,OMA}$$

(18)

MATLAB SIMULATION

Download the MATLAB code here

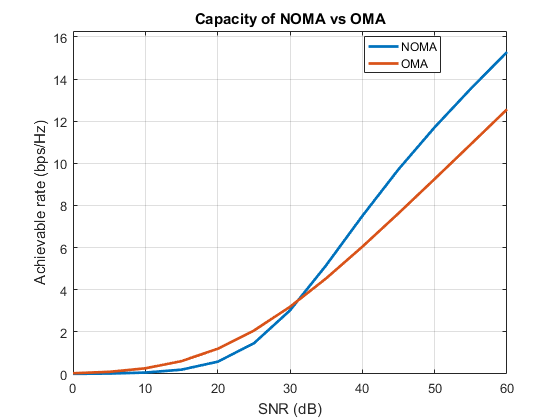
Now that we have the mathematical expressions, let's plot a graph to compare the capacity of OMA and NOMA. Let us consider a network with $N=3$ users and compare their performance. The capacity plots look like this:

We can observe that at low SNR, OMA performs slightly better than NOMA. This is because, NOMA users suffer from interference (due to simultaneous transmission), while OMA users do not experience any such interference. At high SNR, however, NOMA outperforms OMA by offering high capacity. 

In addition, NOMA accomplishes this while utilizing minimal resources. In this example, TDMA requires 3 times slots to complete the whole transmission. If the duration of 1 time slot is 1 ms, TDMA requires 3 ms to complete the transmission. NOMA, on the other hand, completes the transmission in a single time slot itself (i.e., in 1 ms). This significantly reduces the latency. This demonstrates the usefulness of NOMA in future communication technologies.

Reference

"A tutorial on Nonorthogonal multiple access for 5G and beyond," M. Aldababsa et al., Wireless communications and mobile computing, https://doi.org/10.1155/2018/9713450