What is SWIPT (Energy harvesting) NOMA?

As we are moving towards more and more advanced communication systems, the power consumption of devices becomes an important issue. For example, in a wireless network made up of thousands of IoT sensors, drainage of battery may cause the sensors to die. To address this issue, there is a push towards green communication technologies like RF energy harvesting devices.

NOMA requires successive interference cancellation, which as we know, is a computationally intensive task. This places a burden on the battery life. 

When we studied the cooperative NOMA system, we used user cooperation where the near user acted as a relay to the far user. This user cooperation was natural because the near user has the far user's data anyway. But does the near user have enough power to relay that data? What if relaying drains the near user's battery?

This is where RF energy harvesting could help. 

Download the MATLAB code here

What is RF energy harvesting?

There is always electromagnetic signals present everywhere around us due to data transmissions. Of course, these signals make no sense to us unless they contain information that is intended for us. But apart from carrying information for someone else, they also carry power which we can harvest using simple RF circuits. Then, we can make use of this harvested power to make our own transmissions. This way, our battery would never drain.

For a more detailed explanation on the technicalities of energy harvesting, you can refer this excellent paper: ["Power without wires," N. Shinohara, IEEE Microwave Magazine, vol. 12, no. 7, pp. 64 - 73, Dec. 2011]

Types of energy harvesting

There are two main energy harvesting protocols namely, 

1. Time switching
2. Power splitting

Let's briefly see about these two techniques

1. Energy harvesting by Time Switching

Here, the device operates in a time-slotted fashion. During the first fraction of time-slot, the device harvests electromagnetic energy from its surroundings. This harvested power is used for transmission in the next fraction of time-slot. We will see more about time-switching in future posts. In this post, we will see how to implement power-splitting protocol for cooperative NOMA.

2. Energy harvesting by Power Splitting

Here, the device splits the received signal power for energy harvesting and information decoding. Unlike time switching, where separate time slots are required for both the processes, power splitting allows simultaneous implementation of energy harvesting and information decoding. So, this method is also called SWIPT - Simultaneous Wireless Information and Power Transfer.

Next, let's go ahead and take a look at the network model of our cooperative SWIPT NOMA.

Cooperative SWIPT NOMA Network

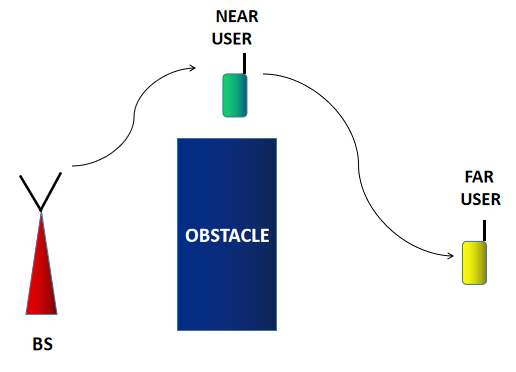
Fig 1: Network model of cooperative SWIPT NOMA

We are considering downlink transmission where, the base station (BS) uses NOMA to simultaneously transmit messages to the near user and far user. Unfortunately, there is an obstacle in the path between the BS and far user which causes extreme shadowing. As a result, the far user cannot receive the signal.

But the near user has a very good channel with the BS. According to NOMA principles, the near user has to first decode the data intended for the far user and then perform SIC to decode its own data. So, the near user has a copy of the far user's information. So, the near user can help the far user by acting as a decode-and-forward relay.

But the problem here is, the near user does not have enough power to relay the data to the far user. Therefore, the near user decides to perform the power-splitting method of energy harvesting a.k.a SWIPT to harvest sufficient power.

We can view the entire transmission to be taking place in two time slots. In the first time slot, the near user receives the data transmitted by the BS. By employing the power splitting protocol, a fraction of the received signal power is harvested and the remaining power is used for information decoding. In the second time slot, the harvested power is used by the near user to relay data to the far user.

Let's look at the signal model next.

Signal model of cooperative SWIPT NOMA

Time slot 1

The NOMA signal transmitted by the BS in the first time slot is given by, $$x = \sqrt{P}\left (\sqrt{\alpha_n}x_n+\sqrt{\alpha_f}x_f\right )$$

where,

• $P$ - Transmit power
• $\alpha_n$ - fraction of power allocated to near user
• $\alpha_f$ - fraction of power allocated to far user
• $x_n$ - signal intended for near user
• $x_f$ - signal intended for far user

Due to extreme shadowing, the far user cannot receive this signal. The signal received by the near user is given by, $$y_n = \sqrt{P}\left (\sqrt{\alpha_n}x_n+\sqrt{\alpha_f}x_f\right )h_{sn} + w_n$$

where,

• $h_{sn}$ - Rayleigh fading coefficient between the BS and near user with zero mean and variance = $d_{sn}^{-\eta}$
• $d_{sn}$ - distance between BS and near user
• $\eta$ - Path loss exponent
• $w_n$ - AWGN with zero mean and variance = $\sigma^2$

From $y_n$, the near user harvests a fraction of power. Let's denote this fraction by $\psi$. This is also called the energy harvesting coefficient. The remaining fraction $(1-\psi)$ is the fraction of power available for information decoding.

So, after energy harvesting, the signal available for information decoding is, $$y_D = \left(\sqrt{1-\psi}\right)y_n + w_{eh} =\left(\sqrt{1-\psi}\right)\sqrt{P}\left(\sqrt{\alpha_n}x_n+\sqrt{\alpha_f}x_f\right)+\left(\sqrt{1-\psi}\right)w_n+w_{eh}$$ 

where $w_{eh}$ is the thermal noise introduced by the energy harvesting circuitry (with zero mean and $\sigma^2$ variance). For simplicity, let's assume energy harvested from $w_n$ is negligible, leading to the following expression for $y_D$, $$y_D=\left(\sqrt{1-\psi}\right )\sqrt{P}\left(\sqrt{\alpha_n}x_n+\sqrt{\alpha_f}x_f\right) + w_{eh}$$ 

From $y_D$, the near user first performs direct decoding of $x_f$. The achievable rate to decode the far user data by the near user is given by, $$R_{nf} = \dfrac{1}{2}log_2\left(1 + \dfrac{P(1-\psi)\alpha_f|h_{sn}|^2}{P(1-\psi)\alpha_n|h_{sn}|^2+\sigma^2}\right)$$

 (1)

After SIC, the achievable rate for the near user to decode its own information is, $$R_n = \dfrac{1}{2}log_2\left(1 + \dfrac{P(1-\psi)\alpha_n|h_{sn}|^2}{\sigma^2}\right)$$

(2)

How much power is harvested?

Since $\psi$ is the fraction of power harvested in the first time slot, the amount of power harvested is given by, $$P_{H}=P|h_{sn}|^2\zeta\psi$$

(3)

 where $\zeta$ is the power harvesting efficiency of the circuitry.

Time slot 2

In the second time slot, the near user relays the data intended to the far user by using the power harvested in the previous slot, $P_{H}$. So, the signal transmitted by the near user is, $\sqrt{P_H}\tilde{x}_f$. The received signal at the far user is, $$y_f = \sqrt{P_H}\tilde{x}_fh_{nf}+w_f$$

 where, $h_{nf}$ is the Rayleigh fading channel between the near user and far user. Now, the achievable rate at the far user is, $$R_f = \dfrac{1}{2}log_2\left(1 + \dfrac{P_H|h_{sn}|^2}{\sigma^2}\right)$$

(4)

How to optimize the power splitting coefficient $\psi$?

In this section, we will derive an expression to obtain the optimal value of $\psi$. The near user must reliably decode the far user data in the first time slot. Only then it can relay the correct data in the next time slot. To ensure this condition, let's set a constraint $$R_{nf}\gt R_f^*$$ where $R_f^*$ is the far user's target data rate. This constraint means that the achievable rate at the near user to decode the far user data must exceed the far user's target rate.

Let's substitute the expression of $R_{nf}$ from (1) in the above condition and solve for $\psi$. 

\begin{align} \dfrac{1}{2}log_2\left(1 + \dfrac{P(1-\psi)\alpha_f|h_{sn}|^2}{P(1-\psi)\alpha_n|h_{sn}|^2+\sigma^2} \right) &\gt R_f^*\\ log_2\left(1 + \dfrac{P(1-\psi)\alpha_f|h_{sn}|^2}{P(1-\psi)\alpha_n|h_{sn}|^2+\sigma^2} \right) &\gt 2R_f^*\\ 1 + \dfrac{P(1-\psi)\alpha_f|h_{sn}|^2}{P(1-\psi)\alpha_n|h_{sn}|^2+\sigma^2} &\gt 2^{2R_f^*}\\ \dfrac{P(1-\psi)\alpha_f|h_{sn}|^2}{P(1-\psi)\alpha_n|h_{sn}|^2+\sigma^2} &\gt 2^{2R_f^*}-1 \end{align}

Let's denote $2^{2R_f^*}-1$ by $\tau_f$. This is the target SINR for the far user. \begin{align} \dfrac{P(1-\psi)\alpha_f|h_{sn}|^2}{P(1-\psi)\alpha_n|h_{sn}|^2+\sigma^2} &\gt \tau_f\\ P(1-\psi)\alpha_f|h_{sn}|^2 &\gt \tau_fP(1-\psi)\alpha_n|h_{sn}|^2 +\tau_f\sigma^2\\ P(1-\psi)\alpha_f|h_{sn}|^2 - \tau_fP(1-\psi)\alpha_n|h_{sn}|^2 &\gt \tau_f\sigma^2\\ P(1-\psi)|h_{sn}|^2(\alpha_f - \tau_f\alpha_n) &\gt \tau_f\sigma^2\\ (1-\psi) &\gt \dfrac{\tau_f\sigma^2}{P|h_{sn}|^2(\alpha_f - \tau_f\alpha_n) }\\ \psi &\lt 1 - \dfrac{\tau_f\sigma^2}{P|h_{sn}|^2(\alpha_f - \tau_f\alpha_n) } \end{align}

To ensure that $\psi$ is less than the value given by RHS, let's modify the above equation as,

$$ \psi = 1 - \dfrac{\tau_f\sigma^2}{P|h_{sn}|^2(\alpha_f - \tau_f\alpha_n) } - \delta$$

where $\delta$ is a very small number (for example, $10^{-6}$). This value of $\psi$ ensures that enough power is available for information decoding in order to meet the far user's target rate.

MATLAB Simulation

Download the MATLAB code here

Next, let's implement our cooperative SWIPT NOMA network in MATLAB. For this simulation, let's set the target rate for both users as 1 bps/Hz. Also we are considering fixed power allocation with $\alpha_n =0.2$ and $\alpha_f=0.8$. As we saw in the post about power allocation, proper choice of target rates and $\alpha_n$, $\alpha_f$ values are required to make the fixed power allocation method work. Depending on the network parameters, I have optimized these values by trial and error. Better performance than this can be obtained by dynamic power allocation schemes.

First, let's plot the achievable rates for the near user and far user, given by equations (2) and (4). We will get a graph like this:

Fig 2: Average achievable rates vs transmit power

As we can observe in Fig 2, the near user's rate is saturated at around 1 bps/Hz while the far user's rate increases. This saturation is due to energy harvesting. Once the far user's data rate is met at the near user, all the remaining power is harvested. Even if the transmit power is increased, the achievable rate at the near user is still limited due to the energy harvesting operation. But the upside here is that, the near user's target rate of 1 bps/Hz is not violated. Thus, this saturation in rate does not lead to much outage to the near user.

As the transmit power increases, the amount of power harvested [as given by eqn (3)] increases. Thus the amount of power with which the far user's data is transmitted in the second slot increases. This leads to increase in the far user's achievable rate.

From Fig 2, we may come to a conclusion that, since the far user experiences higher average achievable rate, he must have the least outage probability. But when we plot and observe the outage graphs, we see something that is totally opposite to our intuition.

Fig 3: Outage performance of cooperative SWIPT NOMA

From Fig 3, we observe that the far user experiences much greater outage than the near user, although he experiences greater achievable rate on average than the near user. Why did this happen? This is because, in Fig 2, we are talking about the average performance. If we plot the instantaneous achievable rates of both the users, we will get a graph like this:

Fig 4: Instantaneous rates

Now we see why the far user has greater outage in spite of having greater achievable rate. Fig 4 is plotted for a transmit power of 20 dBm. We can see that the far user's achievable rate is centered around a value of 3 bps/Hz, which is captured in Fig 2 at 20 dBm. We can also see that the far user's instantaneous achievable rate falls below the target rate value quite a lot of times. As far as outage calculations are concerned, we don't care how greater the achievable rate is. We only count the number of times the instantaneous rate falls below the target rate. This fall is more frequent for the far user. Thus he has poor outage performance.

But for the near user, although he has lesser achievable rate, it is greater than the target rate most of the time. This explains his better outage performance.

In the next posts, we will explore how the time switching protocol works with cooperative NOMA. Thank you!

References

"On the application of SWIPT in NOMA networks," Y. Liu and M. Elkashlan, (chapter 6 from book: Wireless information and power transfer: theory and practice, Wiley Telecom)  (pp. 99 - 120)