User pairing in NOMA

 Hello everyone! In this post, we'll look at the user pairing problem in NOMA. Let's dive straight in!

Download the MATLAB code here

 

What is the user pairing problem in NOMA?

We know that NOMA serves multiple users simultaneously in the same frequency. But how many users can we support in one frequency carrier? We analyzed this question in detail and found the answer in one of the previous posts. There, we concluded that, if the number of users is increased beyond a limit, the sum throughput of the network will actually begin to drop. So, we cannot increase the number of users per carrier indefinitely.

Then what can we do to support all the users? One solution is to employ hybrid NOMA. Hybrid NOMA is a combination of NOMA with any OMA technique. For example, let's consider TDMA+NOMA, as shown in Fig. 1.  Let's say we have a time slot of 4 ms duration. We have to support 4 users within this time slot. Now, TDMA will divide the 4 ms slot into four 1 ms slots and assign one slot to each user. NOMA, will assign the whole 4 ms slot to the four users. As we know, this will increase the SIC complexity and processing delay. Hybrid NOMA, on the other hand, divides the 4 ms slot into two 2 ms slots and assigns two NOMA users to each slot.

Fig. 1: User assignment in different multiple access schemes

As we can see, hybrid NOMA can serve all the users with reduced complexity. We'll see more about hybrid NOMA schemes in future posts. But in this post, the question is, how to pair NOMA users within each available orthogonal resource? Should we pair users as {(1,2),(3,4)} or {(1,3),(2,4)} or {(1,4),(2,3)}? 

Two user pairing strategies in NOMA

First, let's look at our system model

Fig. 2: System model 

As shown in figure 2, let's consider a downlink communication scenario with 4 users. Let $d_1$, $d_2$, $d_3$, $d_4$ denote the distances of U1, U2, U3, U4 respectively from the base station. U1 is the nearest user and U4 is the farthest user. Therefore, their channel conditions are ordered as $|h_1|^2$>$|h_2|^2$>$|h_3|^2$>$|h_4|^2$. We have two orthogonal resource blocks (time/frequency/subcarriers) and we have to assign two users per block. We'll do the user pairing based on the distances.  There are two simple ways to do this:

                    (i) Near-far pairing (N-F)

                    (ii) Near-near, far-far pairing (N-N, F-F)

(i) Near-far pairing (N-F)

In this method, the nearest user to the base station is paired with the farthest user from the base station. The next nearest user is paired with the next farthest user and so on. In our example, U1 is the nearest user and U4 is the farthest user. So, N-F pairing will pair U1 with U4 in one resource block. U2 will be paired with U3 in the next resource block. 

In the first pair of users, U1 is the near user and U4 is the far user. Therefore, we have to choose the power allocation coefficients as $\alpha_1$<$\alpha_4$. So, U1 should perform successive interference cancellation (SIC), while U4 will perform direct decoding. Similarly, in the second pair of users, U2 is the near user and U3 is the far user. Therefore, we have to choose $\alpha_2$<$\alpha_3$. Here, U2 should perform SIC while U3 will perform direct decoding.

The achievable rates for the users in the first pair are, $$R_{1,nf} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_1|h_1|^2}{\sigma^2}\right) (after SIC)$$ 

$$R_{4,nf} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_4|h_4|^2}{P\alpha_1|h_4|^2+\sigma^2}\right)$$

Similarly, for the second pair,

$$R_{2,nf} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_2|h_2|^2}{\sigma^2}\right) (after SIC)$$ 

$$R_{3,nf} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_3|h_3|^2}{P\alpha_2|h_3|^2+\sigma^2}\right)$$

The sum rate of the N-F scheme will be $$R_{nf}=R_{1,nf}+R_{2,nf}+R_{3,nf}+R_{4,nf}$$

(i) Near-near, far-far pairing (N-N, F-F)

Another way to perform user pairing is to group the nearest user with the next nearest user. The farthest user is grouped with the next farthest user. If we follow this strategy, in our example, U1 will be paired with U2 in one resource block. U3 will be paired with U4 in the next resource block.

Now, in the first pair of users, U1 is nearest to the base station when compared to U2. Therefore, we have to choose $\alpha_1$<$\alpha_2$. U1 should perform SIC, U2 will perform direct decoding. Similarly, U3 is closer to the base station than U4. So, we have to choose $\alpha_3$<$\alpha_4$. U3 should perform SIC, while U4 will perform direct decoding.

The achievable rates for the users in the first pair are, $$R_{1,nn} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_1|h_1|^2}{\sigma^2}\right) (after SIC)$$ 

$$R_{2,nn} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_2|h_2|^2}{P\alpha_1|h_2|^2+\sigma^2}\right)$$

Similarly, for the second pair,

$$R_{3,nn} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_3|h_3|^2}{\sigma^2}\right) (after SIC)$$ 

$$R_{4,nn} = \dfrac{1}{2}log_2\left(1 + \dfrac{P\alpha_4|h_4|^2}{P\alpha_3|h_4|^2+\sigma^2}\right)$$

The sum rate of the N-F scheme will be $$R_{nn}=R_{1,nn}+R_{2,nn}+R_{3,nn}+R_{4,nn}$$

MATLAB Simulation

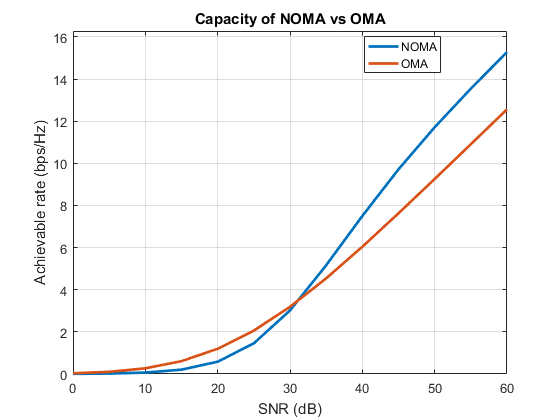
Now that we have seen two different techniques, the natural question that arises is, which one is better? And what if we simply multiplex all the users in the same carrier (SC-NOMA), with no user pairing? And why we need NOMA at all, with all the additional work needed for user pairing? Why not just use TDMA? Let's find out the answer by implementing everything in MATLAB. In this simulation, we consider N = 4 users. We are going to plot the sum rate of the network when we employ each of the user pairing schemes that we studied today. In addition, we are going to compare the sum rate performance of the network with just SC-NOMA and TDMA. 

Download the MATLAB code here

 Some observations:

1. When near user is paired with the far user, a larger sum rate is achieved. This confirms the well-known fact that NOMA performs better when the channel conditions between the two users is distinct [1].

2. When near-near, far-far pairing is used, NOMA still achieves more sum rate than TDMA, but the improvement is not that significant.

3. The performance of SC-NOMA is poor when compared to TDMA! Because, the overloading of all users into the same carrier creates interference issues. This also confirms our observation from this post that we cannot simply increase the number of users sharing the same carrier, without paying a price. 

References

[1] Mahmoud Aldababsa, Mesut Toka, Selahattin Gökçeli, Güneş Karabulut Kurt, Oğuz Kucur, "A Tutorial on Nonorthogonal Multiple Access for 5G and Beyond", Wireless Communications and Mobile Computing, vol. 2018, Article ID 9713450, 24 pages, 2018. https://doi.org/10.1155/2018/9713450

[2] Z. Ding, P. Fan and H. V. Poor, "Impact of User Pairing on 5G Nonorthogonal Multiple-Access Downlink Transmissions," in IEEE Transactions on Vehicular Technology, vol. 65, no. 8, pp. 6010-6023, Aug. 2016, doi: 10.1109/TVT.2015.2480766.